
The function slowly grows to positive infinity as x increases, and slowly goes to negative infinity as x approaches 0 ("slowly" as compared to any power law of x). Conclusion: The product rule of differentiation has strong applications in the field of calculus and engineering science. 1 Derivatives of exponential and logarithmic func-tions If you are not familiar with exponential and logarithmic functions you may wish to consult the booklet Exponents and Logarithms which is available from the Mathematics Learning Centre. The reason is that we know the derivative of any constant term is always zero. Example: The logarithm of the number 1 to any non-zero base is always zero. log b x (log a x) / (log a b) Identity rule The logarithm of any positive number to the same base of that number is always 1. The natural log is the inverse function of the exponential function. log b (x) n n log b (x) Change of base rule. What, then, would be the log 10 42. What is the value of LNE Natural logarithm ln(x) calculator finds the logarithm function result in base e which is approximately 2.718.Natural Logarithm Values Tables. The natural logarithm is usually written ln(x) or log e (x). is he approaching the top of the tree when he is 220 feet from the base 7. If ae, we obtain the natural logarithm the derivative of which is expressed by the formula (lnx)1x.


Natural Log (ln) The Natural Log is the logarithm to the base e, where e is an irrational constant approximately equal to 2.718281828. The differentiation formula can be manipulated in the simplest form when a e because ofln e 1. It can be written as exp( x) or more frequently as e x, where e is the base of the exponential function which has a unit slope at (0,1).Graph of part of the natural logarithm function. What is the derivative of log(e) As we know that: log(e) 1. Related Pages Natural Logarithm Logarithmic Functions Derivative Rules Calculus Lessons. If we put a e in the above formula, then the factor on the right side becomes ln e 1and we get the formula for the derivative of the natural logarithmic function log e x ln x. In other words, it has solution to the differential equation being the same such that, y’ = y.The exponential function which has the property that the slope of the tangent line at (0,1) has the value m 0 = 1 is called the natural exponential function. To find the derivative of a common log function, you could just use the change of base rule for logs: The formula for the derivative of a log of any base other than e is: p Title: Calculus 3.
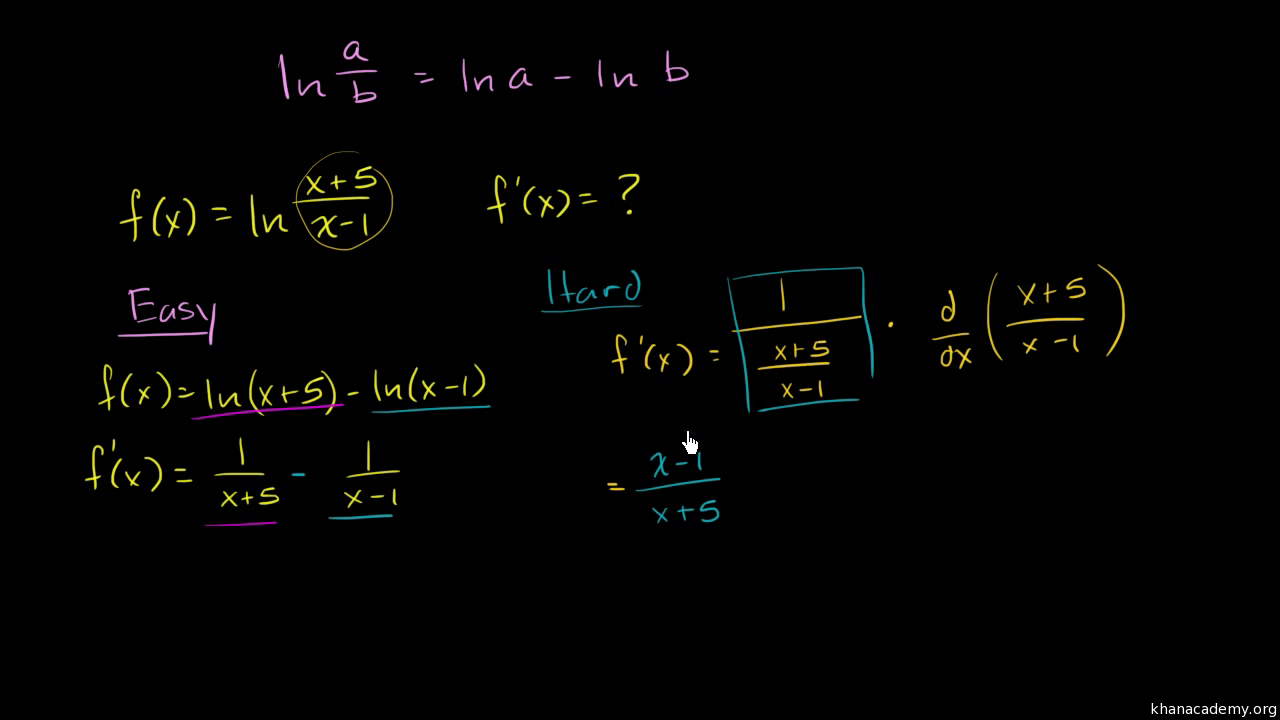
One of the most intriguing and functional characteristics of the natural exponential function is that it is its own derivative. 3.9: Derivatives of Exponential and Logarithmic Functions. Exponential functions can be differentiated using the chain rule.


 0 kommentar(er)
0 kommentar(er)
